Two Body Collision
First, we consider a simple case where only one object rotates after collision.
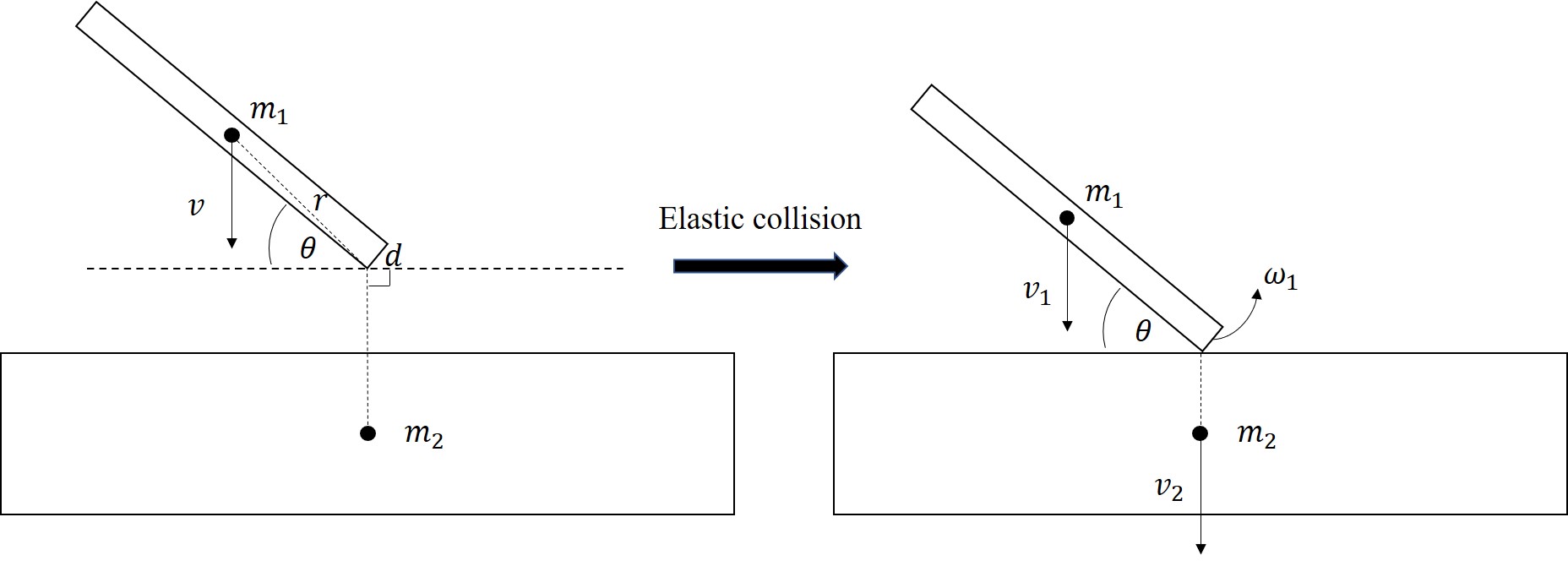
1. Elastic Collision with Rotation
Two rigid bodies collide with rotation, as shown in the figure below.
For elastic collision, the energy and translation momentum are conserved during the collision. So we have,
$$
\begin{align}
\label{eq:momentum}
m_{1}\vec{V} &= m_{1}\vec{V_{1}}+m_{2}\vec{V_{2}}\quad, \\
\label{eq:energy}
\frac{1}{2}m_{1}V^{2} &= \frac{1}{2}m_{1}V_{1}^{2}+\frac{1}{2}m_{1}V_{2}^{2} +\frac{1}{2}I_{1}\omega_{1}^{2}\quad,\\
\end{align}
$$
where $I_{1} = \frac{1}{3}m_{1}(r^2-(\frac{d}{2})^2)$ .
Apply angular momentum theorem, we obtain,
$$
\begin{equation}
\label{eq:angular_momentum}
I_{1}\vec{\omega}_{1} = \vec{r}\times \Delta \vec{P} = \vec{r}\times m_{1}(\vec{V}_{1} - \vec{V}) \quad .
\end{equation}
$$
Suppose $d << r$, then
$$
\begin{align}
|\vec{r}\times m_{1}(\vec{V}_{1} - \vec{V})| &= m_{1}(V_{1}-V)r\cos(\theta) \quad ,\\
I_{1} &= \frac{1}{3}m_{1}r^2\\
\end{align}
$$
Solving equation set $(\ref{eq:momentum},\ref{eq:energy},\ref{eq:angular_momentum})$, we can obtain
$$
\begin{align}
\vec{V_{1}} = \frac{m_{1}+(3\cos(\theta)^2 - 1)m_2}{m_{1}+(3\cos(\theta)^2 + 1)m_2}\vec{V} \quad , \\
\vec{V_{2}} = \frac{2m_1}{m_{1}+(3\cos(\theta)^2 + 1)m_2}\vec{V} \quad ,\\
|\omega_{1}| = \frac{6m_{2}\cos(\theta)|\vec V|}{(m_{1}+(3\cos(\theta)^2 + 1)m_{2})r} \quad .\\
\end{align}
$$
Let $\frac{m_1}{m_2} \to 0$, then
$$
\begin{equation}
\begin{split}
\lim_{\frac{m_1}{m_2} \to 0} \vec{V_{1}} = \frac{3\cos(\theta)^2 - 1}{3\cos(\theta)^2 + 1}\vec{V} \quad , \\
\lim_{\frac{m_1}{m_2} \to 0} |\omega_{1}| = \frac{6\cos(\theta)|V|}{(3\cos(\theta)^2 + 1)r} \quad .\\
\lim_{\frac{m_1}{m_2} \to 0} \vec{V_{2}} = 0 , \\
\end{split}
\end{equation}
$$
2. General Occasion
Before discussing general occasions, we need to discuss some other things.
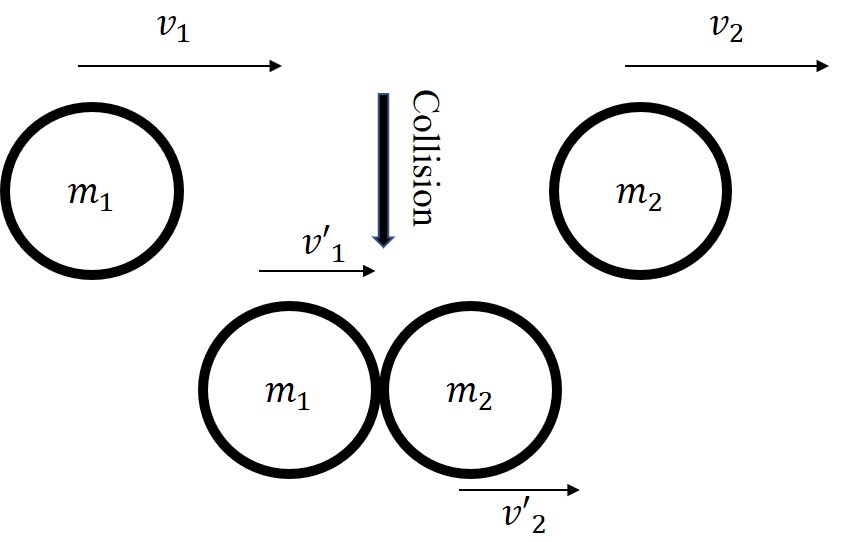
2.1 From Elastic to Inelastic Collision
In collision of two bodies, the total momentum is conserved. That is,
$$
\begin{equation}
\label{eq:momentum_2}
\vec P = m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}} = m_{1}\vec{v^\prime_{1}}+m_{2}\vec{v^\prime_{2}}\quad .
\end{equation}
$$
Before collision total kinetic energy is
$$
E_{k} = \frac{1}{2}m_{1}v_{1}^2 + \frac{1}{2}m_{2}v_{2}^2 \quad .
$$
Total momentum $P$ is conserved in any collision, even if the collision is completely inelastic, so we have sufficient motivation to express $E_{k}$ in terms of $P$ and relative velocity $(v_2 - v_1)$. Kinetic energy becomes
$$
\begin{equation}
\label{eq:cmf_kinetic_energy}
E_{k} = \frac{\vec{P}^2}{2(m_1 + m_2)} + \frac{m_1 m_2 (\vec{v_2} - \vec{v_1})^2}{2(m_1 + m_2)} \quad .
\end{equation}
$$
In fact, the second term is the form of kinetic energy in the center of mass frame. The first item is the kinetic energy of the center of mass. When the system has no external force, it is conserved. (From this perspective, we can understand why the center of mass frame is introduced and why it is important.)
After a totally inelastic collision, the relative velocity $(v^{\prime}_2 - v^{\prime}_1)$ is zero. And the kinetic energy is
$$
E^{\prime}_{k} = \frac{\vec{P}^2}{2(m_1 + m_2)} \quad .
$$
For elastic collision, total kinetic energy is conserved.
$$
\begin{align}
\label{eq:kinetic_energy}
E_{k} = \frac{1}{2}m_{1}v_{1}^2 + \frac{1}{2}m_{2}v_{2}^2 = \frac{1}{2}m_{1}{v^{\prime}}_{1}^2 + \frac{1}{2}m_{2}{v^{\prime}}_{2}^2 \quad .
\end{align}
$$
Bring equation $\eqref{eq:momentum_2}$ into $\eqref{eq:kinetic_energy}$, we have
$$
\begin{equation}
\label{eq:relative_velocity}
\vec{v^{\prime}_{2}} - \vec{v^{\prime}_{1}} = -(\vec{v_2} - \vec{v_1}) \quad .
\end{equation}
$$
So the momentum and kinetic energy conservation equations are
$$
\begin{cases}
\label{eq:state_equations_without_spin}
m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}} = m_{1}\vec{v^\prime_{1}}+m_{2}\vec{v^\prime_{2}} \\
\vec{v^{\prime}_{2}} - \vec{v^{\prime}_{1}} = -(\vec{v_2} - \vec{v_1}) \quad.\\
\end{cases}
$$
When collision is not elastic, the equations become
$$
\begin{cases}
m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}} = m_{1}\vec{v^\prime_{1}}+m_{2}\vec{v^\prime_{2}} \\
\vec{v^{\prime}_{2}} - \vec{v^{\prime}_{1}} = -e(\vec{v_2} - \vec{v_1}) \quad.\\
\end{cases}
$$
Where $e$ is the coefficient of restitution and the range is 0 to 1. In the center of mass frame, $e$ evaluates the relationship between the kinetic energy after and before the collision. From equation $\eqref{eq:cmf_kinetic_energy}$ one can easily show that
$$
\begin{align}
E_{kcm} = \frac{m_1 m_2 (\vec{v_2} - \vec{v_1})^2}{2(m_1 + m_2)} \\
E^{\prime}_{kcm} = \frac{m_1 m_2 (\vec{v^{\prime}_2} - \vec{v^{\prime}_1})^2}{2(m_1 + m_2)} \\
e = \sqrt{\frac{E^{\prime}_{kcm}}{E_{kcm}}} \quad .\\
\end{align}
$$
In a totally inelastic collision, $e = 0$, which means that the (relative)kinetic energy becomes zero after the collision and the relative velocity disappears. On the contrary, if $e = 1$ , kinetic energy is conserved and the relative velocity changes sign.
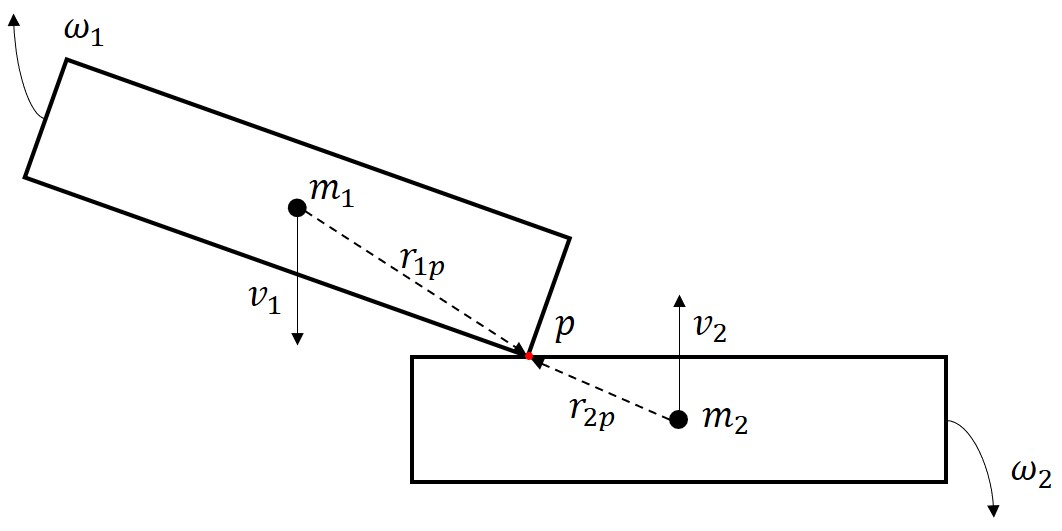
2.2 Collision with Rotation
The total energy $E$ with rotation is
$$
E = \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}+\frac{1}{2}I_{1}\omega_{1}^{2}+\frac{1}{2}I_{2}\omega_{2}^{2} \quad ,
$$
where $I_{1}$ and $I_{2}$ are the moments of Inertia of objects 1 and 2, respectively.
Momentum conservation and angular momentum theorem tell us that
$$
\begin{align}
\label{eq:total_momentum}
m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}} = m_{1}\vec{v^\prime_{1}}+m_{2}\vec{v^\prime_{2}} \\
I_{1}(\vec{\omega^{\prime}_{1}}-\vec{\omega_{1}}) = \vec{r_{1p}} \times \vec{J} \\
I_{2}(\vec{\omega^{\prime}_{2}}-\vec{\omega_{2}}) = \vec{r_{2p}} \times \vec{J} \\
\vec{J} = m_{1}(\vec{v^{\prime}_{1}}-\vec{v_{1}}) = - m_{2}(\vec{v^{\prime}_{2}}-\vec{v_{2}}) \quad .
\end{align}
$$
Where $\vec{r}_{1p}$ and $\vec{r}_{2p}$ are the distances between the impact point $p$ and the center of mass of objects 1 and 2, respectively. $\vec{J}$ is the impulse of object 1 in the collision and the prime symbol indicates the state after the collision.
For elastic collision, total energy $E$ is conserved.
$$
\begin{equation}
\label{eq:total_energy}
\frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}+\frac{1}{2}I_{1}\omega_{1}^{2}+\frac{1}{2}I_{2}\omega_{2}^{2} = \frac{1}{2}m_{1}{v^{\prime}_{1}}^{2}+\frac{1}{2}m_{2}{v^{\prime}_{2}}^{2}+\frac{1}{2}I_{1}{\omega^{\prime}_{1}}^{2}+\frac{1}{2}I_{2}{\omega^{\prime}_{2}}^{2}
\end{equation}
$$
Applying equation $\eqref{eq:total_momentum}$ into $\eqref{eq:total_energy}$, we have
$$
\begin{equation}
\label{eq:relative_velocity_relation}
(\vec{v_{1}} +\vec{\omega_{1}} \times \vec{r_{1p}}) - (\vec{v_{2}} +\vec{\omega_{2}} \times \vec{r_{2p}}) = -((\vec{v^{\prime}_{1}} +\vec{\omega^{\prime}_{1}} \times \vec{r_{1p}}) - (\vec{v^{\prime}_{2}} +\vec{\omega^{\prime}_{2}} \times \vec{r_{2p}})) \quad .
\end{equation}
$$
Velocity of impact point $p$ on body 1 and 2 are
$$
\begin{align}
\vec{v_{1p}} = \vec{v_{1}} +\vec{\omega_{1}} \times \vec{r_{1p}} \quad , \\
\vec{v_{2p}} = \vec{v_{2}} +\vec{\omega_{2}} \times \vec{r_{2p}} \quad . \\
\end{align}
$$
Then equation $\eqref{eq:relative_velocity_relation}$ becomes
$$
\vec{v^{\prime}_{2p}} -\vec{v^{\prime}_{1p}} = -(\vec{v_{2p}}-\vec{v_{1p}}) \quad .
$$
So we get a set of equations similar to $\eqref{eq:state_equations_without_spin}$,
$$
\begin{cases}
m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}} = m_{1}\vec{v^\prime_{1}}+m_{2}\vec{v^\prime_{2}} \\
\vec{v^{\prime}_{2p}} -\vec{v^{\prime}_{1p}} = -(\vec{v_{2p}}-\vec{v_{1p}}) \\
I_{1}(\vec{\omega^{\prime}_{1}}-\vec{\omega_{1}}) = \vec{r_{1p}} \times m_{1}(\vec{v^{\prime}_{1}}-\vec{v_{1}}) \\
I_{2}(\vec{\omega^{\prime}_{2}}-\vec{\omega_{2}}) = \vec{r_{2p}} \times m_{1}(\vec{v^{\prime}_{1}}-\vec{v_{1}}) \quad . \\
\end{cases}
$$
According to section 2.1, when collision is not elastic, the equations become
$$
\begin{equation}
\label{eq:state_equation}
\begin{cases}
m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}} = m_{1}\vec{v^\prime_{1}}+m_{2}\vec{v^\prime_{2}} \\
\vec{v^{\prime}_{2p}} -\vec{v^{\prime}_{1p}} = -e(\vec{v_{2p}}-\vec{v_{1p}}) \\
I_{1}(\vec{\omega^{\prime}_{1}}-\vec{\omega_{1}}) = \vec{r_{1p}} \times \vec{J} \\
I_{2}(\vec{\omega^{\prime}_{2}}-\vec{\omega_{2}}) = \vec{r_{2p}} \times \vec{J} \quad . \\
\end{cases}
\end{equation}
$$
where $e$ is the coefficient of restitution.
-
Solve equations $\eqref{eq:state_equation}$: The force between two bodies at impact point is perpendicular to the contact surface, which means $\vec{J} = |J|\vec{n} \equiv j\vec{n}$. Where $\vec{n}$ is normal to the surface(edge) of body 2 that is being impacted, and pointing outward from body 2. The value of the final state (after collision) is represented by $j$ as
$$
\begin{equation}
\label{eq:final_state_equation}
\begin{cases}
\vec{v^{\prime}_{1}} = \vec{v_{1}} + \frac{j\vec{n}}{m_1} \\
\vec{v^{\prime}_{2}} = \vec{v_{2}} - \frac{j\vec{n}}{m_2} \\
\vec{\omega^{\prime}_{1}} = \vec{\omega_{1}} + \frac{\vec{r_{1p}}\times j\vec{n}}{I{1}} \\
\vec{\omega^{\prime}_{2}} = \vec{\omega_{2}} - \frac{\vec{r_{2p}}\times j\vec{n}}{I{2}} \quad .\\
\end{cases}
\end{equation}
$$Therefore, the only thing left is to solve for j from equations $\eqref{eq:state_equation}$ and $\eqref{eq:final_state_equation}$.
$$
\begin{align}
\vec{v^{\prime}_{2p}} -\vec{v^{\prime}_{1p}} &= -e(\vec{v_{2p}}-\vec{v_{1p}}) \\
(\vec{v^{\prime}_{2p}} -\vec{v^{\prime}_{1p}})\cdot\vec{n} &= -e(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n} \\
((\vec{v^{\prime}_{2}} +\vec{\omega^{\prime}_{2}} \times \vec{r_{2p}}) -(\vec{v^{\prime}_{1}} +\vec{\omega^{\prime}_{1}} \times \vec{r_{1p}}) )\cdot\vec{n} &=
-e(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n} \\
(\vec{v_{2}} - \frac{j\vec{n}}{m_2}+(\vec{\omega_{2}} - \frac{\vec{r_{2p}}\times j\vec{n}}{I_{2}})\times\vec{r_{2p}} - (\vec{v_{1}} + \frac{j\vec{n}}{m_1}) &- (\vec{\omega_{1}} + \frac{\vec{r_{1p}}\times j\vec{n}}{I_{1}})\times\vec{r_{1p}} )\cdot\vec{n} \\
&= -e(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n} \\
(\vec{v_{2p}} - \vec{v_{1p}} - \frac{j\vec{n}}{m_2} - \frac{\vec{r_{2p}}\times j\vec{n}}{I_{2}}\times\vec{r_{2p}} - \frac{j\vec{n}}{m_1} &- \frac{\vec{r_{1p}}\times j\vec{n}}{I_{1}}\times\vec{r_{1p}})\cdot{n} = -e(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n} \\
(- \frac{j\vec{n}}{m_2} - \frac{\vec{r_{2p}}\times j\vec{n}}{I_{2}}\times\vec{r_{2p}} - \frac{j\vec{n}}{m_1} - \frac{\vec{r_{1p}}\times j\vec{n}}{I_{1}}\times&\vec{r_{1p}})\cdot{n} = -(e+1)(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n} \\
\end{align}
$$
Using cross product rules
$$
(\vec{A} \times \vec{B})\cdot \vec{C} = (\vec{B}\times\vec{C})\cdot\vec{A} \quad ,
$$
and $\vec{n}^{2}=1$ we have,
$$
j(-\frac{1}{m_{1}} -\frac{1}{m_{2}}-\frac{(\vec{r_{1p}}\times \vec{n})^2}{I_{1}}-\frac{(\vec{r_{2p}}\times \vec{n})^2}{I_{2}}) = -(1+e)(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n} \quad.
$$
Finally,
$$
j = \frac{(1+e)(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n}}{\frac{1}{m_{1}}+\frac{1}{m_{2}}+\frac{(\vec{r_{1p}}\times \vec{n})^2}{I_{1}}+\frac{(\vec{r_{2p}}\times \vec{n})^2}{I_{2}}}
$$
When body 2 is a wall or ground, we can let $m_{2} \to \infty$ and $I_{2} \to \infty$ and $j$ becomes
$$
j = \frac{(1+e)(\vec{v_{2p}}-\vec{v_{1p}})\cdot\vec{n}}{\frac{1}{m_{1}}+\frac{(\vec{r_{1p}}\times \vec{n})^2}{I_{1}}} \quad .
$$
References
- Vadim Kaplunovsky, Notes on Elastic and Inelastic Collisions, The University of Texas at Austin.
- myPhysicsLab, Rigid Body Collisions, https://www.myphysicslab.com/engine2D/collision-en.html.
- Ladislav Kavan, Rigid Body Collision Response, Charles University.